SOLIDWORKS Motion es la herramienta de simulación de dinámica de cuerpo rígido dentro de SOLIDWORKS. Esto quiere decir que es posible analizar el movimiento de los cuerpos, pero no su deformación: los cuerpos son considerados infinitamente rígidos (no deformables).
SOLIDWORKS Motion permite analizar trayectorias, dimensionar motores (torque, consumo de energía), observar efectos de fricción, diseño de levas, diseño de resortes y demás componentes que provoquen movimientos.
Los resortes son elementos esenciales en el diseño de mecanismos. Su diseño puede acelerarse mediante el uso SOLIDWORKS Motion. En esta entrada observaremos a través de un simple ejemplo las consideraciones a la hora de diseñar un resorte.
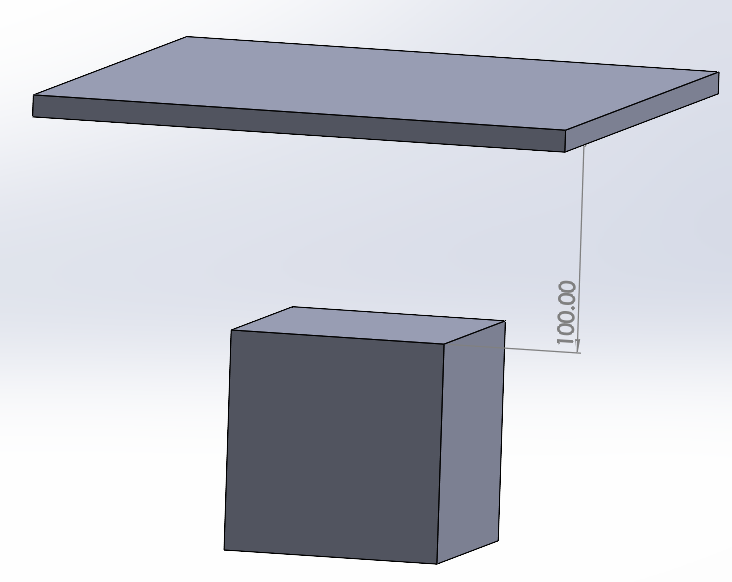
Para ello utilizaremos el siguiente ensamble, compuesto de una placa que se encuentra fija y de un cubo de masa 1 kg. Observa que la separación inicial entre la cara inferior de la placa y la cara superior del cubo es de 100 mm.
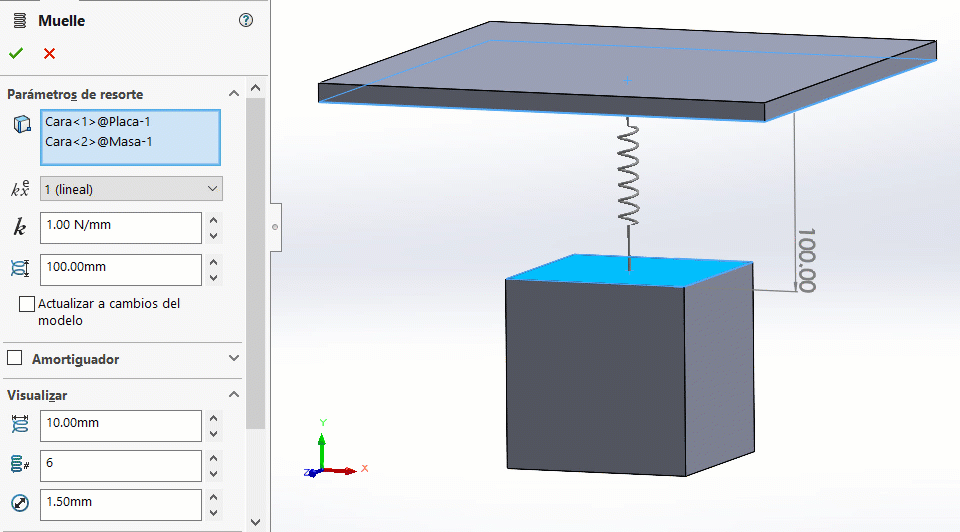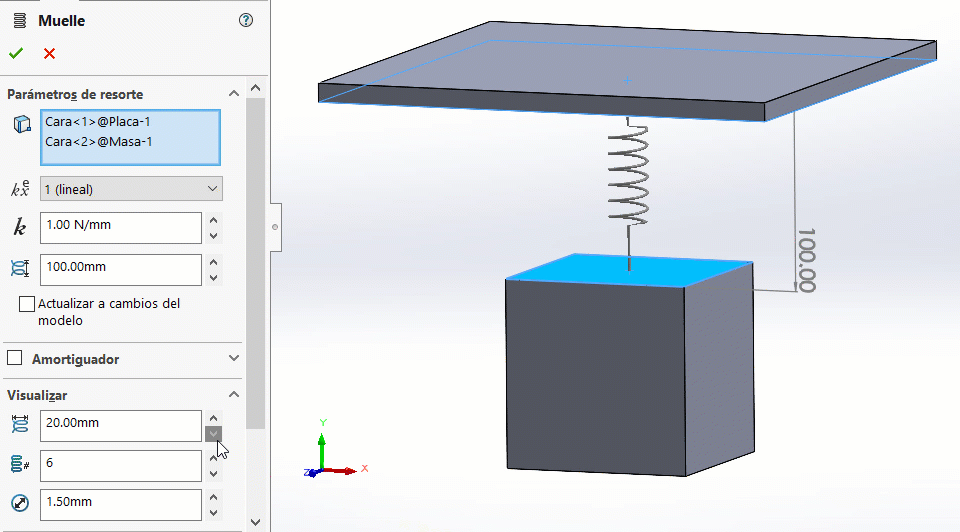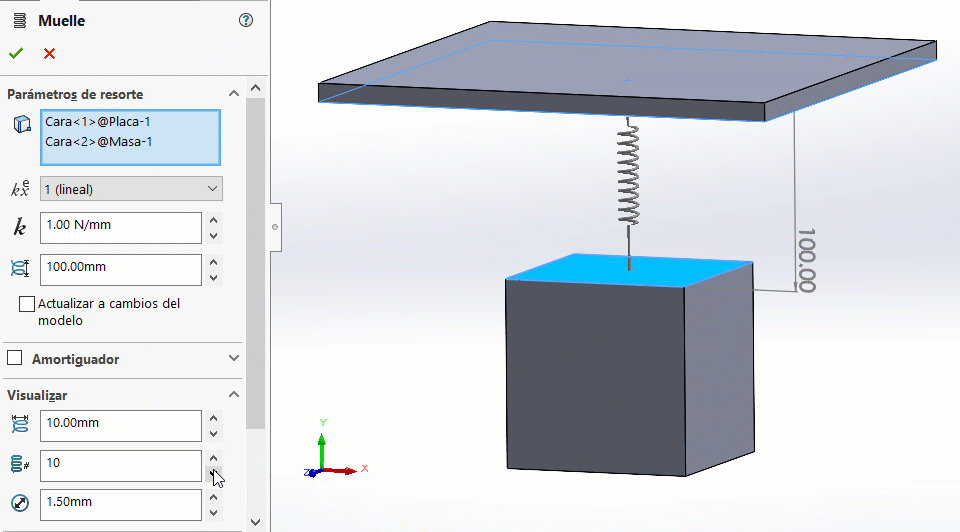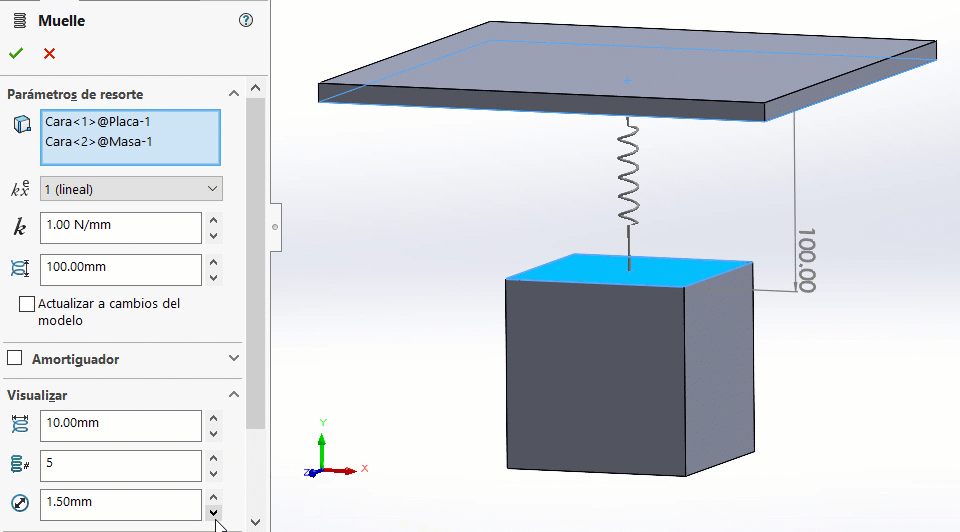
Definiremos un resorte entre las caras mencionadas anteriormente. Observa los siguientes parámetros:
→ k= constante de resorte.
En su forma más simple, recuerda que el comportamiento de un resorte está dado por la ley de Hooke:
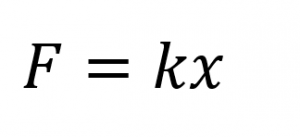
Donde:
F= Fuerza aplicada.
k= constante del resorte.
x= desplazamiento (posición final-posición inicial)
→ Longitud libre: es la medida del resorte en estado de reposo. Observa que se estable en 100 mm automáticamente (distancia real entre las caras seleccionadas). A través de la longitud libre se pueden agregar precargas:
a) Si para este ejemplo la longitud libre la pusiéramos en 110mm, estaríamos expresando un estado inicial de compresión. El resorte en estado libre mide 110mm y ahora se encuentra en 100 mm, por lo que tiene 10 mm de compresión. Nota que el efecto del resorte sería regresar a su estado original, por lo que empujaría el peso hacia abajo.
b) Si para este ejemplo, la longitud libre la pusiéramos en 90mm, estaríamos expresando un estado inicial de compresión. El resorte en estado libre mide 90 mm y ahora se encuentra a 100mm, por lo que tiene 10 mm de tensión. Nota que el efecto del resorte sería regresar a su estado original, jalaría el peso hacia arriba.
→ El campo de visualizar únicamente aplica a aspectos visuales del resorte. Las modificaciones que se hagan en los parámetros de esta sección NO tienen efecto en el comportamiento mecánico del resorte.
Simularemos el fenómeno por 5 segundos. Observa los resultados:
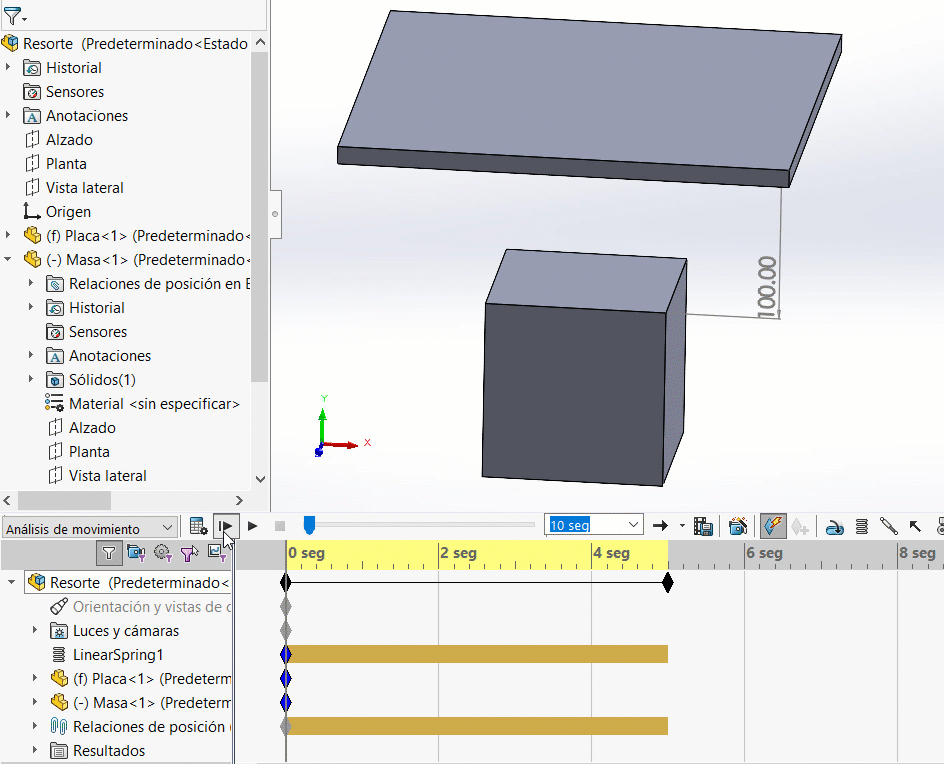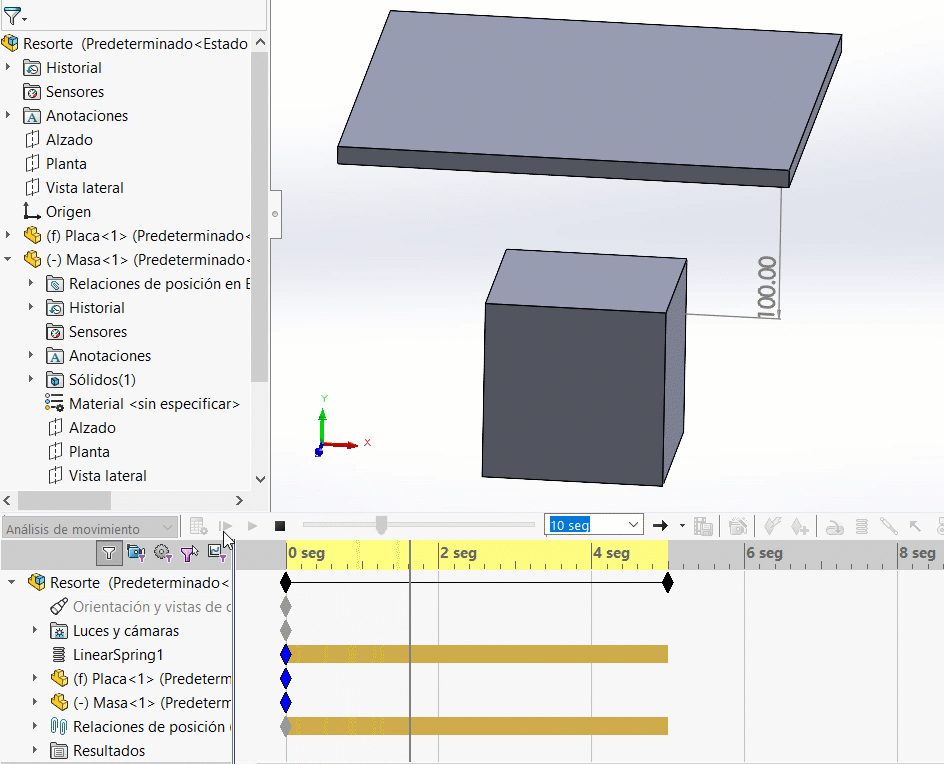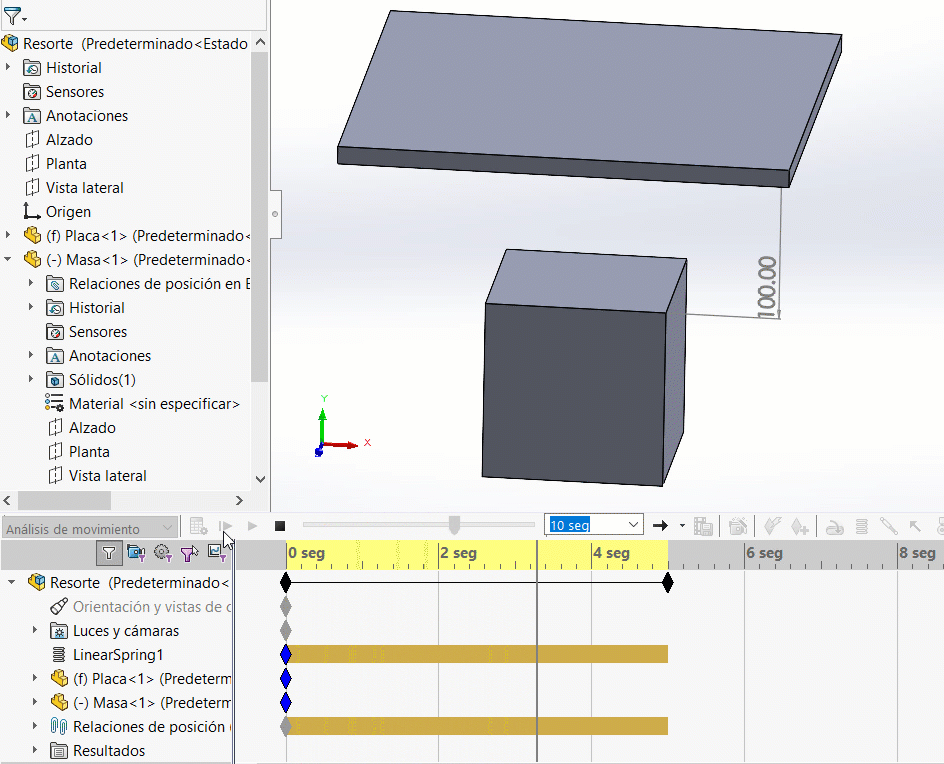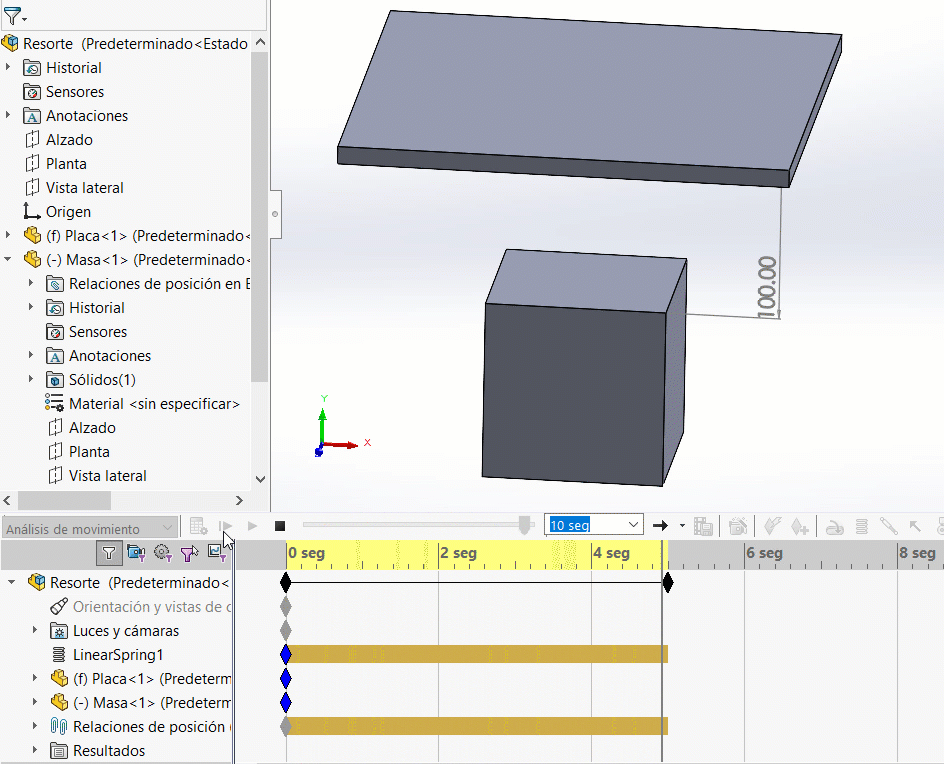
En efecto, ¡no hay movimiento! Esto debido a que no hay ninguna fuerza que inicie el movimiento. Recuerda que el resorte está en estado libre (ninguna precarga). ¡Nos hace falta el efecto de la gravedad! Agregando la gravedad observa los resultados:
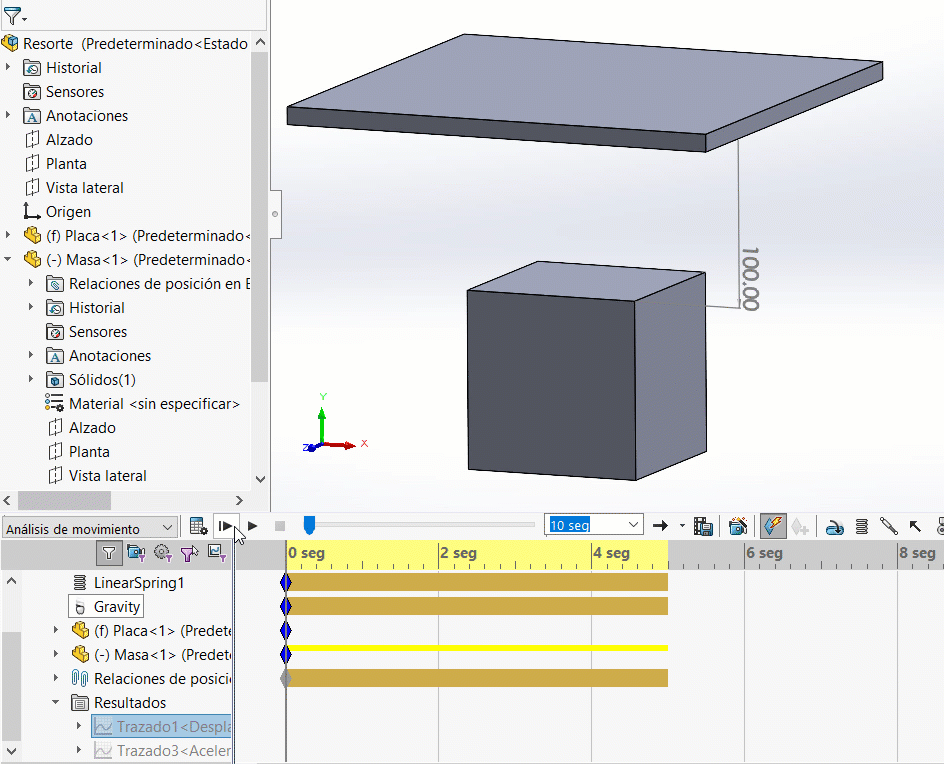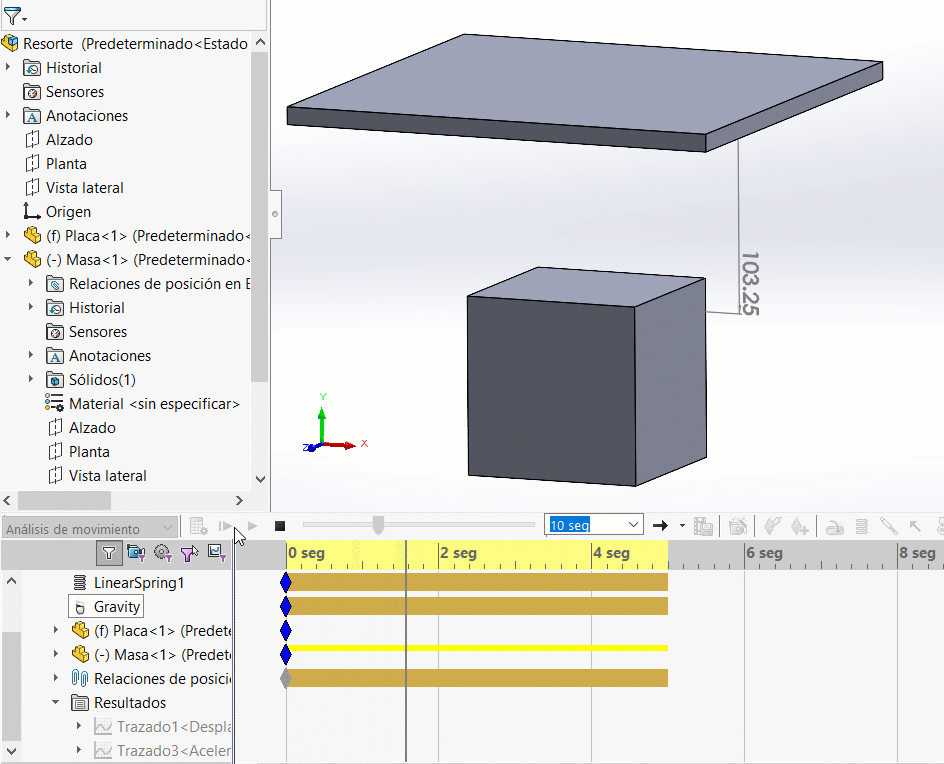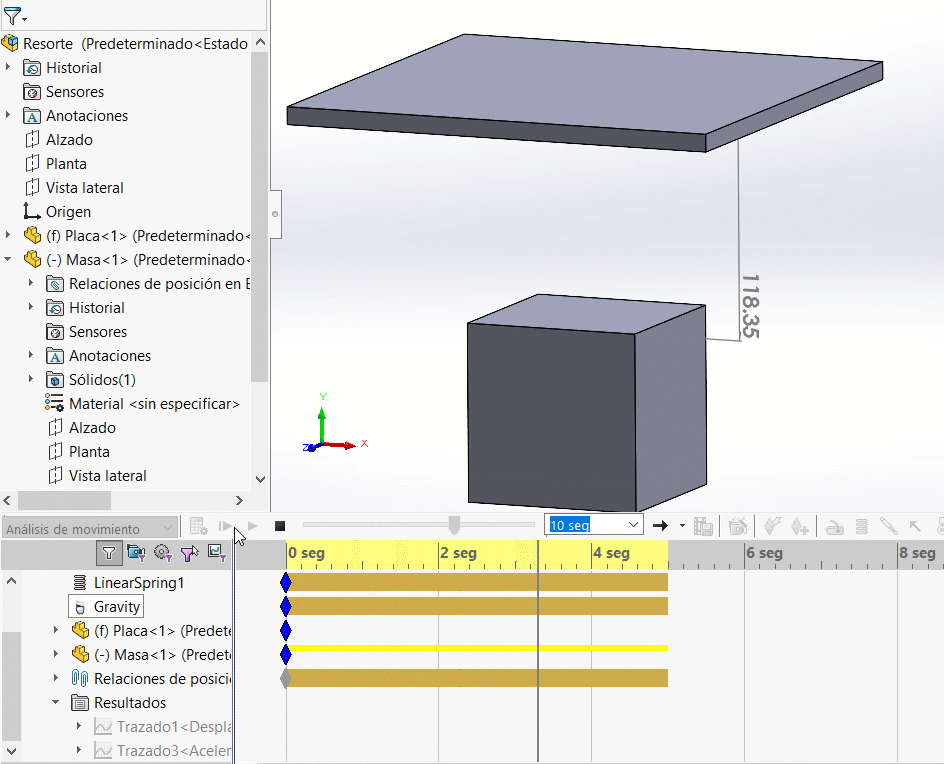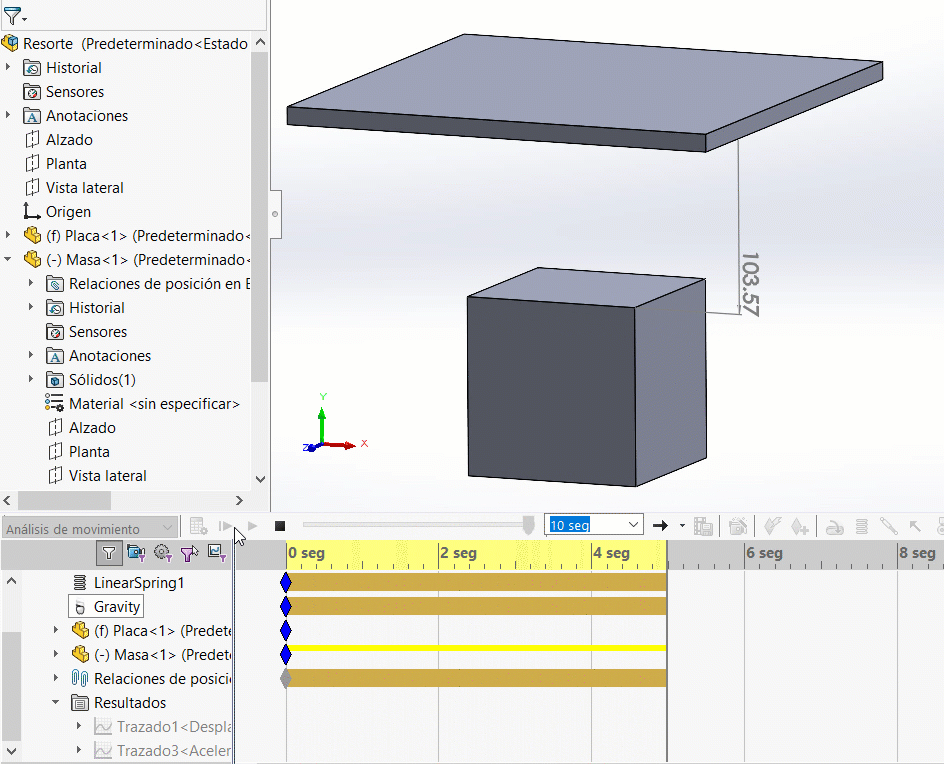
Analizando el gráfico de desplazamiento vertical, podremos observar un comportamiento sinusoidal: el resorte baja 20mm y sube de nuevo esos 20mm. Una oscilación con amplitud de 20 mm. (SOLIDWORKS Motion calcula desplazamientos en los centros de masa de los cuerpos. Cuando el cubo está a una distancia de 100 mm de la placa, el centro de masa del cubo está distanciado a 206 mm del origen del ensamble)
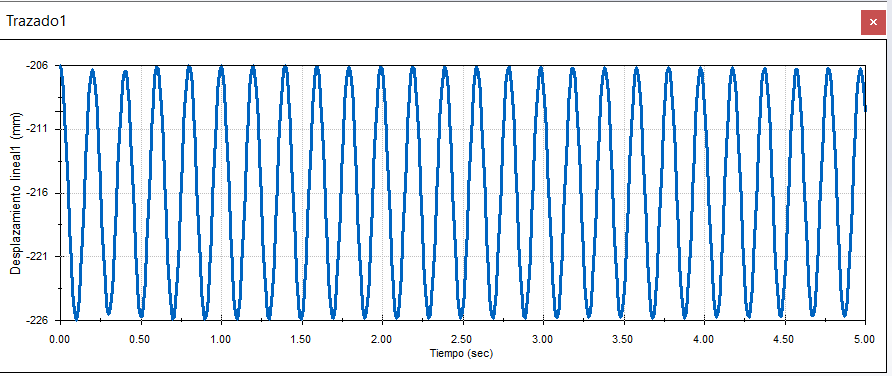
Este resultado es válido en las condiciones aplicadas, sin embargo esto NO sucede en la realidad. Sabemos que en algún momento ese movimiento se detendrá, el sistema no estará oscilando infinitamente (¡qué alegría que sí! ¡Las máquinas de movimiento perpetuo fuesen una realidad!)
De alguna forma debemos agregar una forma de pérdida de energía, con el fin de tener el comportamiento esperado. La respuesta a esto es ¡el amortiguamiento! Todos los materiales presentan un nivel de amortiguamiento, el cual absorbe energía y estabiliza los sistemas.
De la ecuación de resorte podemos calcular cuál es la elongación que esperamos del resorte:
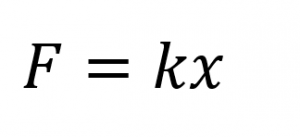 La fuerza es el peso de la pieza, que resulta de multiplicar la masa por la gravedad:
La fuerza es el peso de la pieza, que resulta de multiplicar la masa por la gravedad:
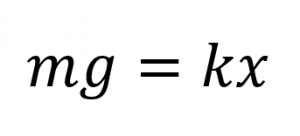
Sustituyendo, tendremos:
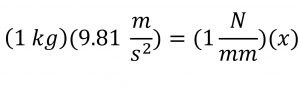
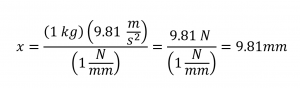
Esperamos que debido a la masa de 1 kg, el resorte se elongue 9.81 mm, terminando en una distancia entre la placa y el cubo de 109.81 mm.
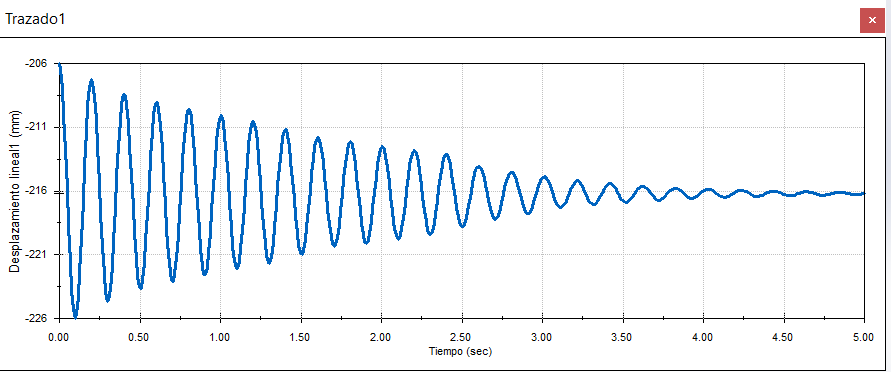
Agregaremos un amortiguamiento de 0.001 N/(mm/s), observa los resultados:
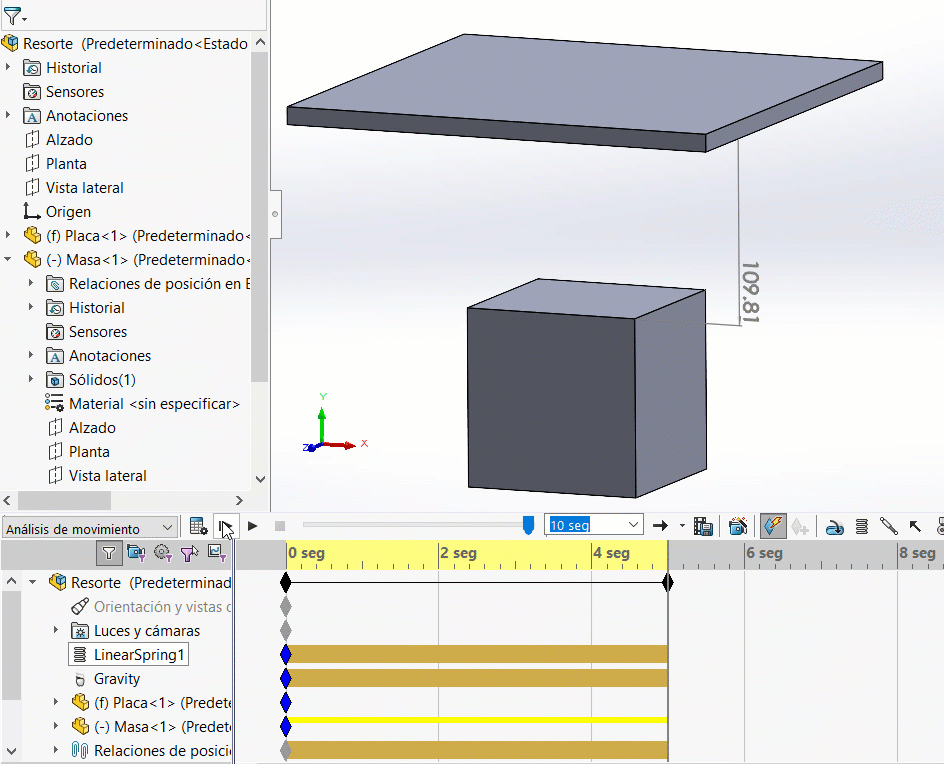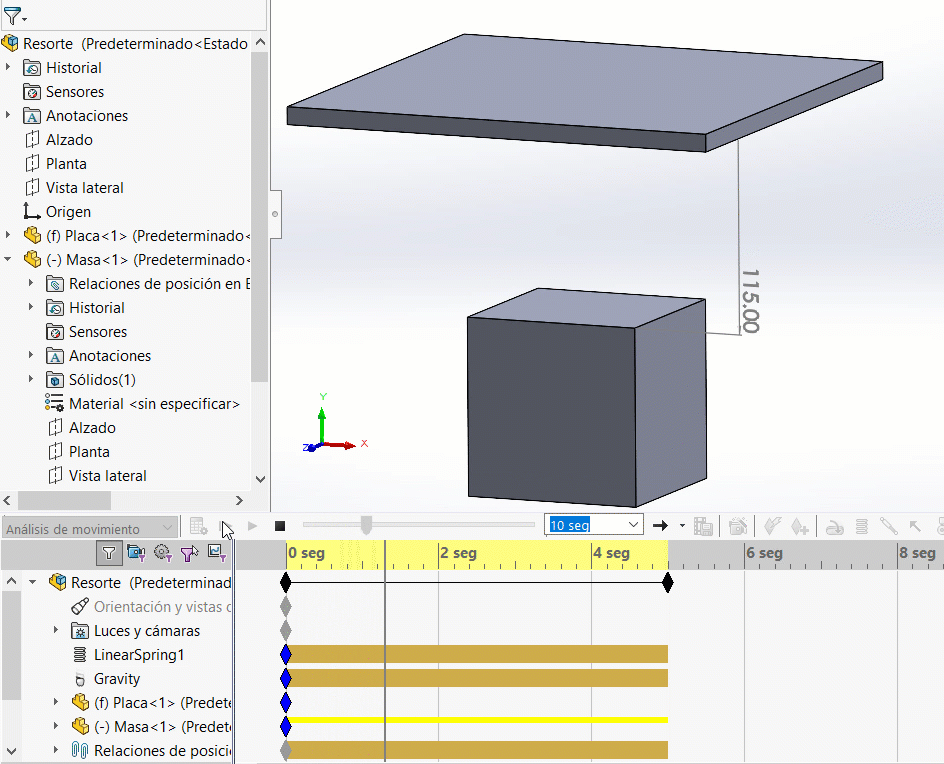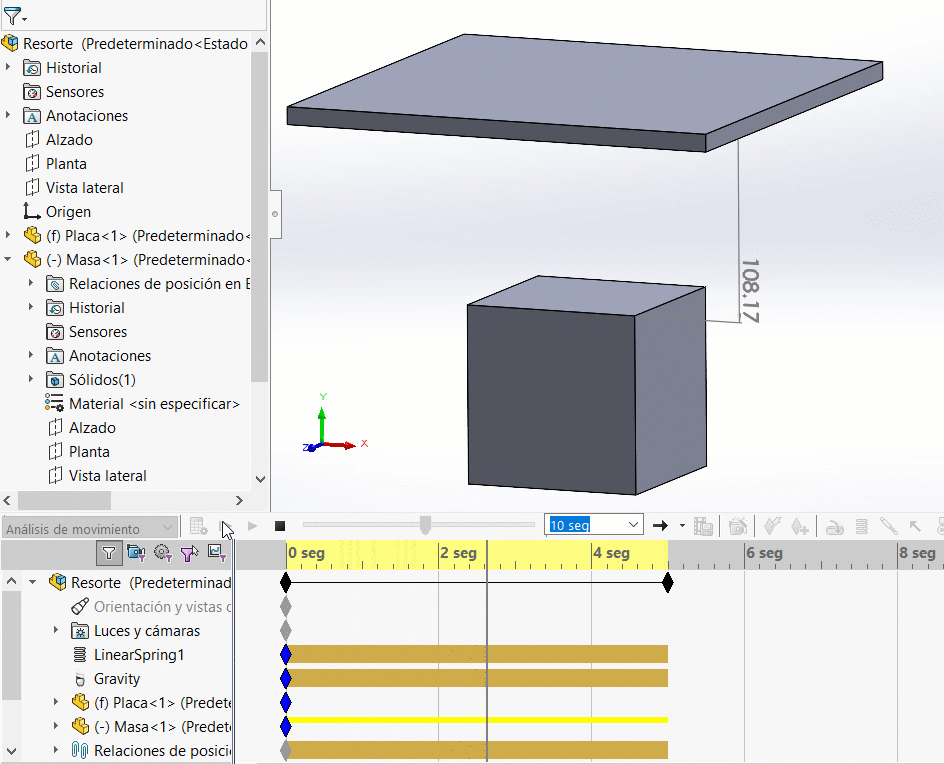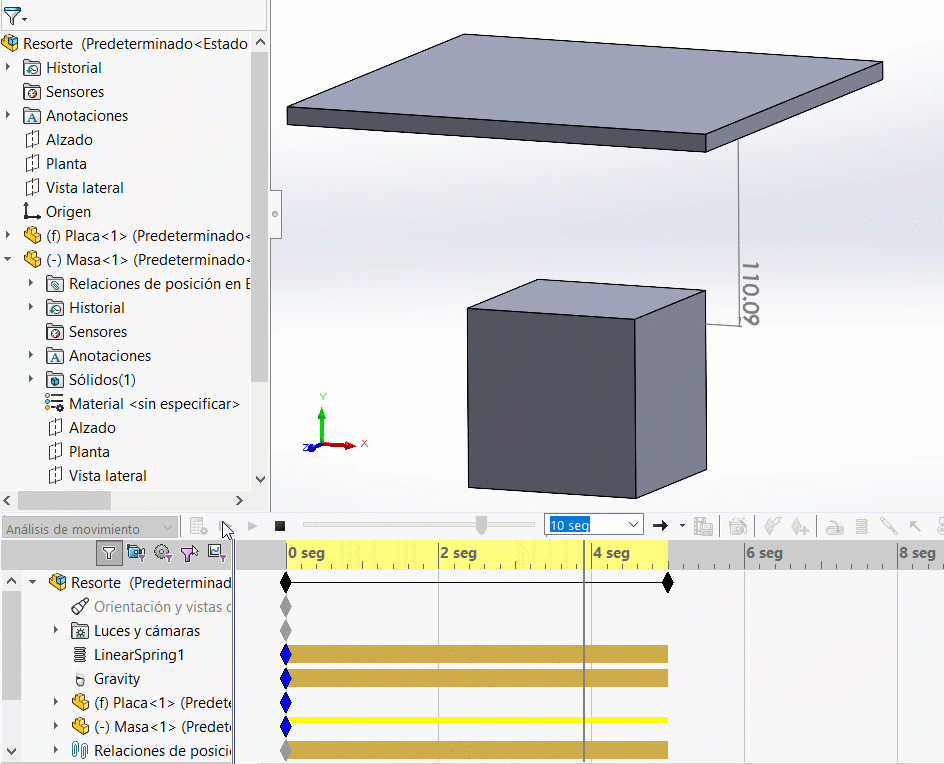
Observa como se estabiliza en un desplazamiento de 215.81 mm, la diferencia es de 9.81 mm.
¡Coincide con nuestro cálculo teórico!
Observa el efecto del amortiguamiento en la disipación de la energía:
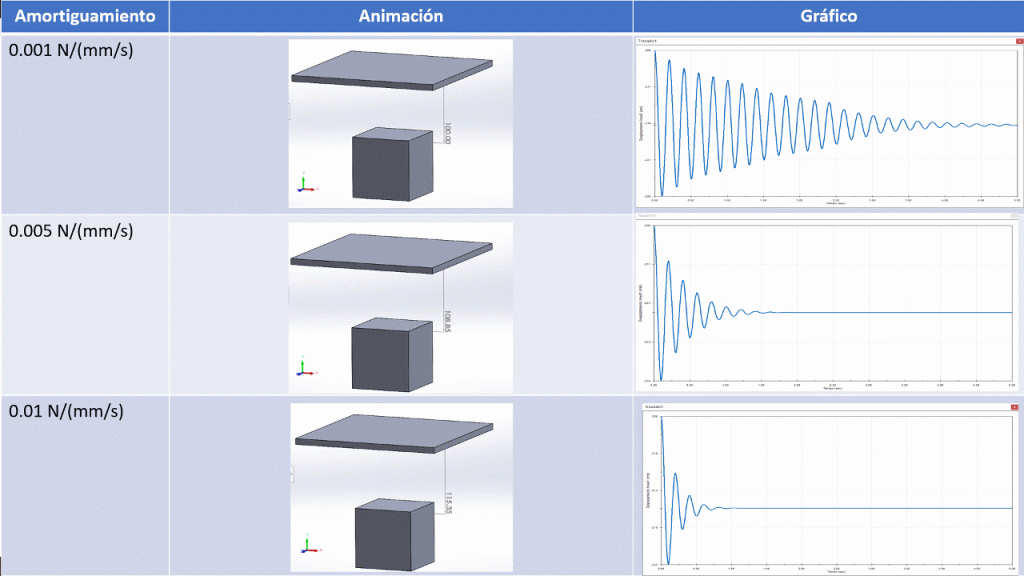
Podrás notar que el valor de amortiguamiento entre cada experimento aumenta linealmente, pero el resultado no responde linealmente. Realmente el efecto de los resortes está descrito por ecuaciones diferenciales, por lo que no responden linealmente. ¡Nuestro mundo es completamente no lineal! Sin embargo, hacemos simplificaciones para hacernos más fácil la vida.
Por último, la máxima aceleración también es posible de predecirse mediante ecuaciones.
¿Recuerdas la segunda ley de Newton?
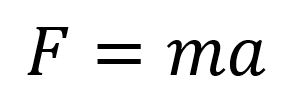
Podrás notar que tanto la segunda ley de Newton como la ley de Hooke relacionan fuerzas, por lo que podemos igualar ambas ecuaciones:
![]()
Despejando la aceleración:
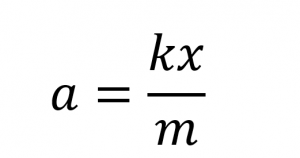
Sustituyendo tenemos que la máxima aceleración es de:
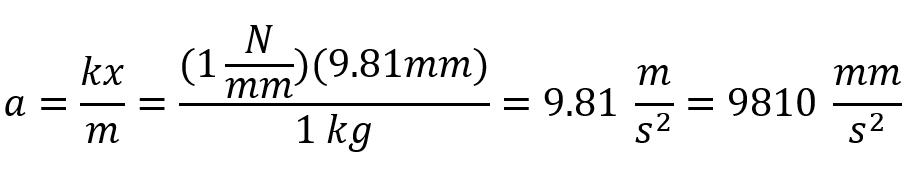
SOLIDWORKS Motion nos confirma este valor. La máxima aceleración siempre se logrará no importa que valor de amortiguamiento.
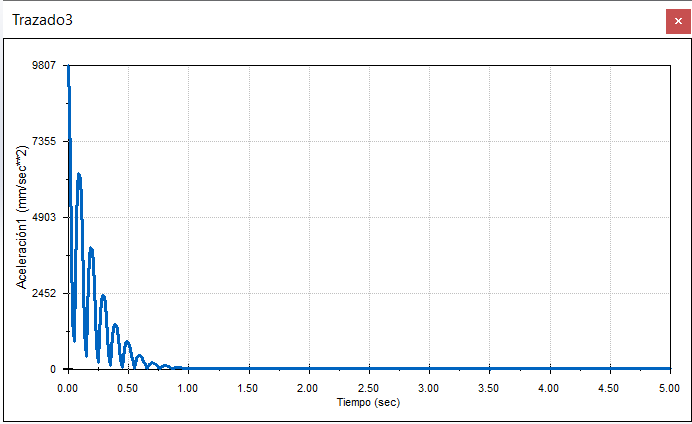
SOLIDWORKS Motion es una herramienta confiable que nos ayuda a realizar validaciones de movimiento. Hemos demostrado que los resultados que arroja tienen correlación con las ecuaciones que rigen el movimiento de los cuerpos rígidos.
Por último, te compartimos el ejercicio para que puedas practicar. ¡Adelante!